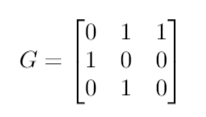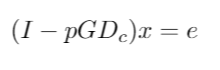page ranking purdue
7:08 AM on Wednesday, November 25th, 2020 (West Lafayette, IN)
Recently in my numerical methods course at Purdue, we’ve been discussing ways of solving linear systems. Prior to the start of the semester, I was reading the textbook for the course when I came across an interesting concept called document ranking and the vector space model. I did a quick little write up about it here. Within that section of the book, it also talked about Google’s PageRank algorithm. At the time I didn’t have the capacity to go into it in depth, but it’s been very neat to see the class circle around to this concept that was hinted at in the beginning chapters. It’s a concept that interested me from the moment I read about it. Within my numerical methods course, we had an assignment to rank pages from a network of Harvard links, and to find the top 10 pages using Matlab. This was quite fun, and inspired me to repeat this process, but for a network of 100 websites linked to the Purdue page, “https://www.purdue.edu”. I’ve portioned this article into little blurbs explaining each part of the code I wrote, that also detail the PageRank algorithm as we learned it in class. Here goes nothing:
Part 1: The graph
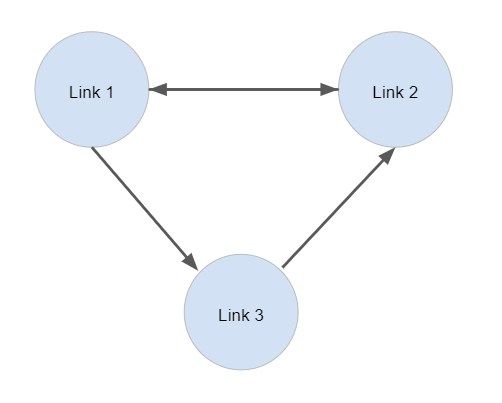
The first step was to obtain a list of the first 100 links that connect to the aforementioned Purdue page, and construct a graph that details their linkages. I chose to go with an adjacency matrix representation, where we store the connectivity information in a 2D matrix. The indices of the rows correspond to different links; row 0 is to link 0 as row 1 is to link 1. From there, the entries in the various columns represent connectivity information; a 1 at index [i,j] means that the link of row i contains the link of column j, somewhere on it. Perhaps that wasn’t as succinct as I would have liked it to be, so below is an example that hopefully clarifies this concept:
On the left, we have an example adjacency matrix for a digraph that represents the connections for 3 links. On the right is the digraph it represents. As we can see, Link 1 has 1’s in the columns that correspond to Links 2 and 3, and thus in the digraph we see that Link 1 points to Links 2 and 3. Examination of the digraph and adjacency matrix further confirms how we will represent connectivity. Note that in this representation, no link has a ‘self loop’; this means that for our model, no link will contain itself. This corresponds to the diagonal entries of our adjacency matrix to consist of all 0’s.
So, this is the representation we want. How do we actually get this data?
Part 2: Web Scraping
When we did this assignment in class, we did it in Matlab, since it has all the linear algebra functions we needed already built in. Matlab is great for math; Cleve Moler made sure of that. While Matlab can accomplish some nifty webscraping practices, I decided to go with Python for this project. With NumPy, I would be able to get all the wonderful linear algebra functions I needed. With beautifulsoup4, I would be able to easily scrape the links from my desired sites, and construct a digraph from their connections easily. Finally, the nail in the coffin: Python is 0-indexed, unlike Matlab.
So, we now have everything we need installed and ready to go; we now need to start writing the code we need. Essentially, what we need is a way to view all the links listed on the html of an input link. Then, we can iteratively move down this list of links, returning a new list per link until we have hit our desired cardinality of 100. For this, I created two functions: createGraph(), and getLinks(). Below is the Python code for createGraph():
def createGraph(url, n):
global U
U = [0]*n
hash_list = [0]*n
G = [[0 for x in range(n)] for y in range(n)]
m = 0
U[m] = url
hash_list[m] = getHash(url)
for j in range(n):
print('Accessing Link Number ', end='');
print(j, end=' ')
print(': ', end='')
print(U[j])
links = getLinks(U[j])
if links != []:
for link in links:
loc = -1
for i in range(m):
if hash_list[i] == getHash(link):
if (link in U[i] and len(link) == len(U[i])):
loc = i
break
if (loc == -1 and m < n-1):
m = m + 1
U[m] = link
hash_list[m] = getHash(link)
loc = m
if (loc >= 0):
G[loc][j] = 1
return GAs you can discern, this function takes 2 arguments: a string that constitutes the desired origin URL, and a number n, that denotes the dimension of the graph that is ultimately returned. From there, we define a global array called U; this will end up holding the strings of the n URLs that correspond to the returned graph. We then define a hash_list, for easy referencing of the URL strings stored in U, as well as a 2D matrix G which will store our connectivity information.
We then add the initial URL that is passed in as an argument, and begin our crawl through the interwebs. For each new link, until we fulfil our space constraint of n links, we get every link that is listed on that page. Then, we iterate through this list. If the link has already been cataloged, and thus has an associated column index, we simply update the graph with a 1 to indicate the connection. If the link has not been cataloged, we add it to the array of URLs, and assign it a hash, and then update the graph.
In this way, we are able to crawl through the links attached to the input URL until we obtain a graph of the desired size, at which point we return the corresponding adjacency matrix.
Below is the hash function I used to simplify access/recognition of the URLs:
def getHash(url):
sum = 0;
for i in range(len(url)):
sum += ord(url[i])
return len(url) + 1024*sumThere is just one crucial part left for this function to work as intended: the return of the associated URLs listed on an input URL. To do this, I wrote a function, shown below, that takes a single URL as a parameter. From there, it attempts to get the HTML associated with the page. If the request is not successful, it returns an empty array of links which the calling function createGraph() handles. If the request is successful, an empty array of links is initialized, and beautifulsoup4 is used to return a list that can be scanned for links. For each item in this list, we check if it has the attribute ‘href’. If it does, I ensure it has no string ‘tel’, as early on this resulting in telephone numbers being returned which was not desirable. Then, if the link includes ‘https’, it is added to the array of links that will eventually be returned. One final thing I had to do, which is noted in the code below, is add some code to handle something I noticed with the Purdue web infrastructure. The main page, ‘https://www.purdue.edu/’, would sometimes be linked on other pages as ‘//www.purdue.edu/’. This meant that my program would register this as a separate URL, when it fact it should be coupled with the original main page. Thus, if I found a link of this form, I attached the ‘https:’ so that it would match the intended format, and not be double counted.
def getLinks(url):
http = httplib2.Http()
try:
status, response = http.request(url)
except:
print('Error getting page. Moving on.')
return []
links = []
for link in BeautifulSoup(response, parse_only=SoupStrainer('a'), features="html.parser"):
if link.has_attr('href'):
if not('tel' in link['href']):
if 'https' in link['href']:
links.append(link['href'])
# elif to handle weird Purdue network anomaly
elif ('//' in link['href'] and not ('http' in link['href'])):
links.append('https:' + link['href'])
return linkspart 3: Actually doing something with it
This is where the linear algebra comes in; we have all this information, and now we just need to make sense of it. For this purpose, we are going to work with the matrix from Part 1, and demonstrate with a simple example the set of operations that we must perform.
The first step, is to construct a new matrix, Dc(we will omit fancy subscripts so that you can match these names to those used in the code). Dc is a diagonal matrix whose entries consist of 1 divided by the column sums of our original digraph adjacency matrix, which we will call G. Both are given below:
The next couple of steps are still simple, but the associated ‘why’ becomes a bit more blurred; for this purpose, I am going to speak about the PageRank algorithm at a high level and not get caught up in the details of the ‘why’. The main idea, is that we can model a series of websearches by a random walk from each page in our graph, G. We can pick a probability p, that will be the probability that a random walk results in the clicking of a link that is listed on the page. Thus, 1-p is the probability that some random page is chosen instead of clicking a link from the current page. We can then use this to construct a transition probability matrix. After some mathematical manipulation of an equation involving our transition probability matrix of a Markov chain that represents the random walk of the user, we arrive at the following:
(In the future I hope to post an article detailing how we got to this equation, but for now it’s not important.)
In the equation above, I is an identity matrix of the same dimension as G. P represents our probability as discussed above, G and Dc are the same, and e is a column vector of 1’s. The last step now, is to solve for x, which will give us the ranking of our URLs based on the connections in G, as well as our chosen probability of 0.85. For something with such complex origins, it boils down wonderfully to a simple math problem any sixth grader could sort out.
Now, we’re ready to jump into the last necessary function, pageRank(), which is given below:
def pageRank(G, n):
G = np.array(G)
D = np.zeros((n, n))
colSums = np.sum(G, 0)
for i in range(n):
D[i, i] = colSums[i]
Dc = np.zeros((n, n))
for i in range(n):
if D[i, i] == 0:
Dc[i, i] = 0.0
else:
Dc[i, i] = 1.0 / D[i, i]
I = np.identity(n)
e = np.ones((n, 1))
pGDc = G.dot(Dc)
pGDc = pGDc * 0.85
result = I - pGDc
x = solve(result, e)
indices = x.argsort(0)
print('\n')
print('Results Printed Below: ')
print('\n')
count = 1
for i in range(n-1,0,-1):
print('#', end='');
print(count, end='');
print(' Rank Value: ', end='');
print(str(x[indices[i]]), end='')
print(' URL: ', end='')
print(str(np.array(U)[indices[i]]), end='')
print('\n')
count = count + 1The input parameters for this function are the digraph adjacency matrix G, as well as the dimension of G, given by n. From there, we use NumPy to convert the 2D array into the standard data type NumPy uses to perform linear algebra operations. We also initialize a nxn matrix of zeros for our column sums, and use the NumPy function sum() to obtain the column sums of G. From there, we initialize our matrix Dc, which will store 1 divided by the corresponding column sum for each of its diagonal entries. This is accomplished by the for-loop you see to the left; if the column sum is 0, we leave it alone, as dividing by 0 would result in error, otherwise we go forward with the computation.
Next up, we create the other necessary components for our computation:
Identity matrix I of the same dimension as G
e, our column vector of 1’s that has the same number of rows as G
Then, we compute the relevant part of the the left hand side of the equation given above, which is our identity matrix minus our probability times the product of our matrices G and Dc.
Finally, we use NumPy to solve the equation above for x, which is a column vector that ranks our pages; a higher value corresponds to a higher rank. In addition to this, we use NumPy to sort our indices, so that we may form a correspondence between the ranked URLs and their corresponding URL strings.
Finally, the program prints out the top 10 pages, and their corresponding URL.
Below are the results that I found:
#1 Rank Value: [[9.21338764]] URL: ['https://www.purdue.edu']#2 Rank Value: [[6.77607646]] URL: ['https://www.purdue.edu/disabilityresources/']#3 Rank Value: [[5.84282071]] URL: ['https://www.purdue.edu/directory/']#4 Rank Value: [[5.28089884]] URL: ['https://www.purdue.edu/purdue/giveNow.html']#5 Rank Value: [[5.21939596]] URL: ['https://www.purdue.edu/purdue/commercialization/index.php']#6 Rank Value: [[4.93934603]] URL: ['https://www.purdue.edu/securepurdue/security-programs/copyright-policies/reporting-alleged-copyright-infringement.php']#7 Rank Value: [[4.87223517]] URL: ['https://www.purdue.edu/marketing/']#8 Rank Value: [[4.84837967]] URL: ['https://www.purdue.edu/purdue/ea_eou_statement.php']#9 Rank Value: [[4.71570977]] URL: ['https://one.purdue.edu']#10 Rank Value: [[4.31497709]] URL: ['https://www.purdue.edu/boilerconnect/']They seem reasonable, and align with the pages that would have the highest likelihood of being most visited when started at the Purdue homepage.
conclusion
This was a really fun project, and I liked it a lot because it was a nice mix of CS, math, webscraping, and learning new stuff. At first, my results were totally skewed because I jumped right into NumPy without learning how to properly use it. I then went back and properly learned NumPy, and things were so much easier. In the future, I might try to extend this to a nice visualizer; I envision a nice digraph of page links that uses color to convey which pages are ranked higher, and which paths within the digraph are more likely to be take.
Below is the full script(code can also be found here):
import httplib2
from bs4 import BeautifulSoup, SoupStrainer
import numpy as np
from scipy.linalg import solve
# returns a list of all the links that
# are listed on an input URL
def getLinks(url):
http = httplib2.Http()
try:
status, response = http.request(url)
except:
print('Error getting page. Moving on.')
return []
links = []
for link in BeautifulSoup(response, parse_only=SoupStrainer('a'), features="html.parser"):
if link.has_attr('href'):
if not('tel' in link['href']):
if 'https' in link['href']:
links.append(link['href'])
# elif to handle weird Purdue network anomaly
elif ('//' in link['href'] and not ('http' in link['href'])):
links.append('https:' + link['href'])
return links
# hash function for URL indexing
def getHash(url):
sum = 0;
for i in range(len(url)):
sum += ord(url[i])
return len(url) + 1024*sum
# creates and returns an nxn adjacency matrix of the connections
# between the pages linked on the input URL. Iteratively
# finds links until n are found
def createGraph(url, n):
global U
U = [0]*n # to store the URLs
hash_list = [0]*n
G = [[0 for x in range(n)] for y in range(n)] # adjacency matrix
m = 0
U[m] = url
hash_list[m] = getHash(url)
# walk lists of linked links and add them to G
for j in range(n):
print('Accessing Link Number ', end='');
print(j, end=' ')
print(': ', end='')
print(U[j])
links = getLinks(U[j])
if links != []:
for link in links:
loc = -1
# determine is URL is already logged
for i in range(m):
if hash_list[i] == getHash(link):
if (link in U[i] and len(link) == len(U[i])):
loc = i
break
# if URL is not already logged, add it
if (loc == -1 and m < n-1):
m = m + 1
U[m] = link
hash_list[m] = getHash(link)
loc = m
# update G
if (loc >= 0):
G[loc][j] = 1
return G
# takes an input of an nxn adjacency matrix G
# that represents the page connections and
# runs PageRank on them; prints out links in order
def pageRank(G, n):
G = np.array(G)
D = np.zeros((n, n))
colSums = np.sum(G, 0)
for i in range(n):
D[i, i] = colSums[i]
# create matrix Dc
Dc = np.zeros((n, n))
for i in range(n):
if D[i, i] == 0:
Dc[i, i] = 0.0
else:
Dc[i, i] = 1.0 / D[i, i]
I = np.identity(n)
e = np.ones((n, 1))
pGDc = G.dot(Dc)
pGDc = pGDc * 0.85
result = I - pGDc
# compute order, sort
x = solve(result, e)
indices = x.argsort(0)
# print out results
print('\n')
print('Results Printed Below: ')
print('\n')
count = 1
for i in range(n-1,0,-1):
print('#', end='');
print(count, end='');
print(' Rank Value: ', end='');
print(str(x[indices[i]]), end='')
print(' URL: ', end='')
print(str(np.array(U)[indices[i]]), end='')
print('\n')
count = count + 1
if __name__ == '__main__':
G = createGraph('https://www.purdue.edu', 100)
pageRank(G, 100)bonus
The thumbnail for this article is a visualization of the graph G that was created in Matlab.