building intuition for proving big-oh

8:30 AM on Monday, August 9th, 2021 (West Lafayette, IN)

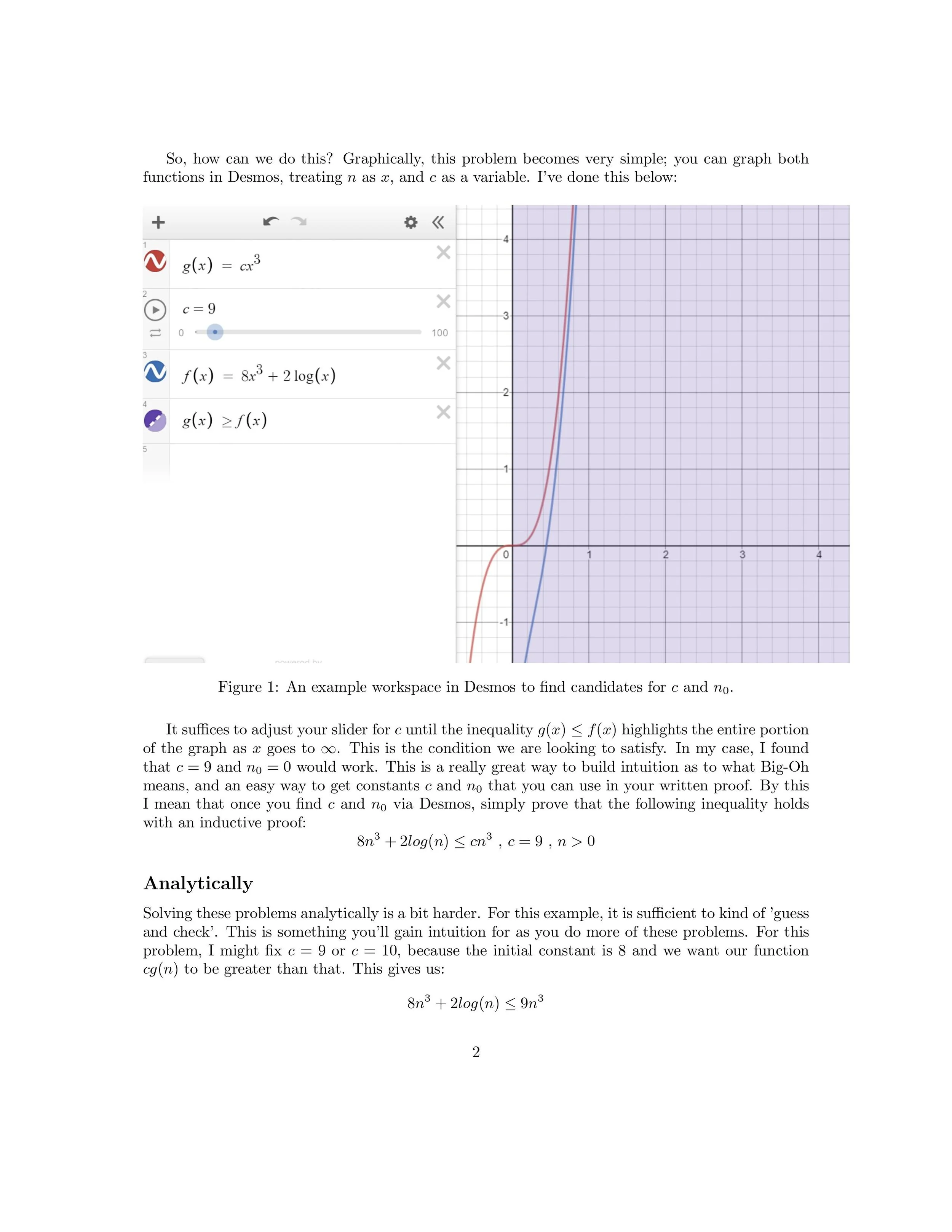
This past semester, I was a TA for CS 240, but I often got questions pertaining to the content of CS 182, which is Purdue’s introductory class to discrete math for CS students. I often got questions regarding the topic of proving a Big-Oh bound for a particular function (and implicitly, runtime), so around the beginning of the semester I bottled up some quick notes I could share with students who were grappling with the topic. Most of them were quite good at doing the actual proof; the stumbling point was figuring out what to prove, given that the definition of a Big-Oh bound comes across as somewhat nebulous and convoluted given all of the notation it includes. Below is the PDF of the notes I jotted down, and the PDF is also linked here.